Grand icosidodécaèdre adouci inversé

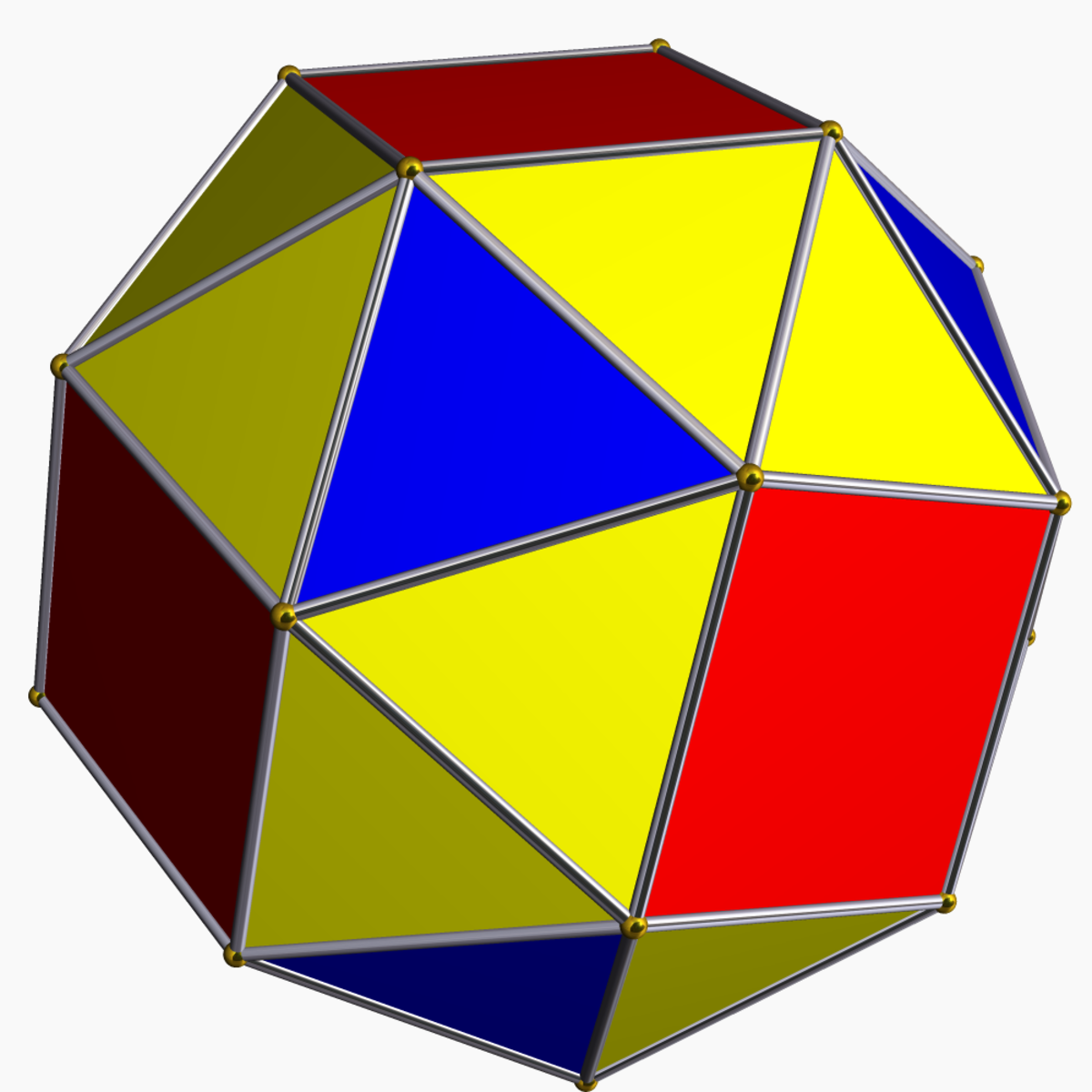
En géométrie, le grand icosidodécaèdre adouci inversé est un polyèdre uniforme non convexe, indexé sous le nom U₆₉.

Coordonnées cartésiennes

Les coordonnées cartésiennes des sommets d'un grand icosidodécaèdre adouci inversé centré à l'origine sont les permutations paires de

(±2α, ±2, ±2β),

(±(α−βτ−1/τ), ±(α/τ β−τ), ±(−ατ−β/τ−1)),

(±(ατ−β/τ 1), ±(−α−βτ 1/τ), ±(−α/τ β τ)),

(±(ατ−β/τ−1), ±(α βτ 1/τ), ±(−α/τ β−τ)) et

(±(α−βτ 1/τ), ±(−α/τ−β−τ), ±(−ατ−β/τ 1)),

avec un nombre pair de signes plus, où

α = ξ−1/ξ

β = −ξ/τ 1/τ²−1/(ξτ),

où τ = (1 √5)/2 est le nombre d'or (quelquefois écrit φ) et ξ est la plus grande solution réelle positive de ξ³−2ξ=−1/τ, ou approximativement 1,2224727. En prenant les permutations impaires des coordonnées ci-dessus avec un nombre impair de signes plus, cela donne une autre forme, l'énantiomorphe de ce polyèdre.